由自積分型 Rogowski 線圈頻率特性分析可以看出線圈輸出波形與被測(cè)電流波形高頻部分比較接近，但是低頻失真較嚴(yán)重，因此可以采用系統(tǒng)辨識(shí)方法對(duì)輸出波形的低頻失真進(jìn)行數(shù)字補(bǔ)償。
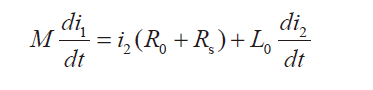
式1
A. 系統(tǒng)辨識(shí)原理
對(duì)于一個(gè)系統(tǒng)，在輸入輸出數(shù)據(jù)的基礎(chǔ)上，從一組給定的模型類(lèi)中，確定一個(gè)與所測(cè)系統(tǒng)等價(jià)的模型，這種方法叫辨識(shí)。辨識(shí)方法是在實(shí)際應(yīng)用中獲取系統(tǒng)模型的最為重要的手段之一，也是數(shù)學(xué)模型和實(shí)際應(yīng)用聯(lián)系的紐帶[5][8]。測(cè)量系統(tǒng)輸入信號(hào)為 x(k)，測(cè)得數(shù)據(jù)用 z(k)表示，則系統(tǒng)離散輸出誤差(OE) 模型可表示為
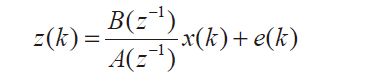
式2
(2) 式中，A(z7):B(z)傳遞函數(shù): e(k)為誤差項(xiàng)。整個(gè)系統(tǒng)的輸出誤差 (OE) 模型如圖 1 所示
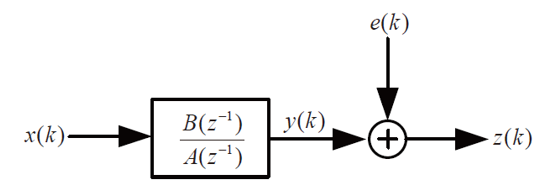
圖 1 輸出誤差 (OE) 模型的系統(tǒng)圖
辨識(shí)就是通過(guò)某種算法，利用模型輸出與實(shí)際輸出問(wèn)的誤差不斷糾正模型參數(shù)，最終得到最優(yōu)模型的過(guò)程。最小二乘類(lèi)辨識(shí)方法，在這種辨識(shí)方法中，首先給出模型的結(jié)構(gòu)，在結(jié)構(gòu)框架下確定系統(tǒng)模型的最優(yōu)參數(shù)。這類(lèi)具有格式規(guī)范的辨識(shí)方法可以演繹成遞推形式，已經(jīng)漸漸替代了經(jīng)典的辨識(shí)算法，成為多數(shù)研究者所采用的方法。
B基于Rogowski 線圈測(cè)量的系統(tǒng)辨識(shí)方法
圖2
一般可認(rèn)為方波包含所有頻段的信息，因此可用方波來(lái)校正測(cè)量系統(tǒng)。首先將 Rogowski 線圈裝入脈沖電流發(fā)生器的輸出回路，調(diào)節(jié)沖擊電流發(fā)生器的參數(shù)，讓其輸出2ms 的方波脈沖，同時(shí)對(duì) Rogowski 自積分回路的采樣電阻和沖擊電流發(fā)生器的分流器上的電壓值進(jìn)行采樣測(cè)量。將采樣數(shù)據(jù)轉(zhuǎn)化為標(biāo)準(zhǔn)的電流輸入輸出測(cè)量值 ,()yo()，所以可以假定校正系統(tǒng)的輸入和輸出分別為u(k) = y (k) 、y(k) = u (k) 。
假定校正系統(tǒng)為線性、時(shí)不變系統(tǒng)，則系統(tǒng)輸入u(t) 、未知權(quán)函數(shù)k()、理論輸出 Z()可表示為:
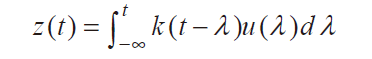
式3
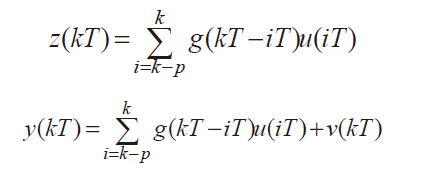
式4
為了求得 p 個(gè)脈沖響應(yīng)值 G={g(0)，g2),...,gp)}T，方波輸入取得的 N組數(shù)據(jù)代入上式可得 N-p+1 個(gè)方程組成的方程組，寫(xiě)成向量形式即是:
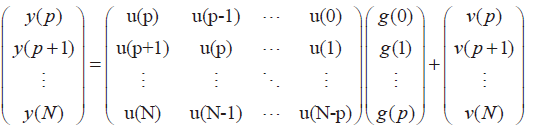
式5
式5即是 Y=UG+V.理論輸出值與實(shí)際輸出值之間的誤差為 V=Y-UG。通過(guò)最小二乘法來(lái)求取脈沖響應(yīng)序列 G:設(shè)定誤差指標(biāo)為:
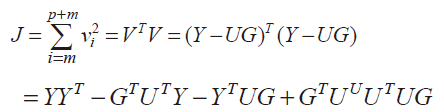
式6
將J對(duì) G微分并令結(jié)果為零，解得 G-(UTUUTY，可求得出一組 G令誤差指標(biāo)J最小，解得
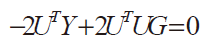
式7
從而得出脈沖響應(yīng)的最小二乘估計(jì) G(UTU-UTG。脈沖響應(yīng)序列 G={g(1),g(2),...,g(p)} 構(gòu)造 Hankel 矩陣，式中 1為 Hankel 矩陣的階數(shù)，k 為 Hankel 矩陳中選用的第一個(gè)脈沖響應(yīng)值的序號(hào)，它決定了由哪些脈沖響應(yīng)值來(lái)構(gòu)成 Hankel矩陣，它可以在 1到 p-l+2之間選擇。
根據(jù)脈沖響應(yīng)函數(shù)與傳遞函數(shù)的關(guān)系，有 1>n 時(shí)rank[H(l.k)]=n，對(duì)于 1>n+1.理論上矩陣行列式的值應(yīng)該為零，在實(shí)際應(yīng)用中，由于存在噪聲誤差，矩陣行列式的值不會(huì)實(shí)際為零，但是會(huì)顯著減小。首先計(jì)算各階 Hankel矩陣行列式的平均值
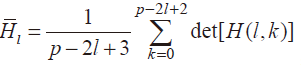
然后計(jì)算平均值的比值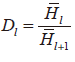
，當(dāng)觀察到
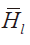開(kāi)始明顯減小，同時(shí)D1顯著增大時(shí)即可判定，此時(shí)的 1 值即為校正系統(tǒng)傳遞函數(shù)的階數(shù) n;或者利用另外一種更直接判定方式，計(jì)算 D1的值，凸的第一個(gè)極大值對(duì)應(yīng)的 1 值就等于校正系統(tǒng)傳遞函數(shù)的階數(shù) n。
當(dāng) p>2n 時(shí)，考慮誤差，根據(jù) Z-n相同次數(shù)的系數(shù)相等，我們可以得到兩組方程組，寫(xiě)成向量形式即是
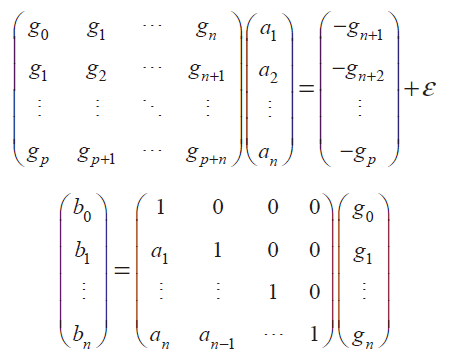
式9
將 (9) 式簡(jiǎn)寫(xiě)為 G1A1=G2+ e，B=A2G3，然后利用最小二乘估計(jì)來(lái)求取系數(shù) A1={al,a2,...,an}:
誤差 e = GA G，設(shè)定誤差指標(biāo)為 J= ee =A,GGIAATG,-GGA;+GG2，將J對(duì) A求微分并令結(jié)果為零，可求出求出一組系數(shù)列 {al,az,··.,a}令 J 最小，求得系數(shù)A=(GIG)TG,G。將求得的系數(shù)al,a2,....an?代入 B-A,G3 可得系數(shù){bo,bi,·.,b小。校正系統(tǒng)的脈沖傳遞函數(shù)為.
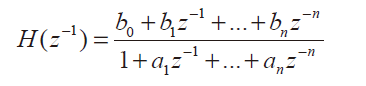
式11
c、校正方法檢驗(yàn)
采用上述 Rogowski 線圈辨識(shí)方法后，對(duì)比測(cè)量電流波形與輸入電流波形的吻合程度，以及對(duì)比未采用系統(tǒng)辨識(shí)方法前后輸出電流波形與輸入電流波形的吻合程度，如圖4 所示，在采用系統(tǒng)辨識(shí)方法校正前，輸入波形和輸出波形在波頭部分(頻率較高) 吻合度較高，但是在波尾部分(頻率較低) 失真嚴(yán)重:如圖 5 所示，采用系統(tǒng)辨識(shí)方法后，測(cè)量波形和輸入波形在波頭和波尾部分吻合度都較高。經(jīng)對(duì)比試驗(yàn)可以發(fā)現(xiàn)采用系統(tǒng)辨識(shí)后可以大大改善Rogowski 線圈低頻失真程度。
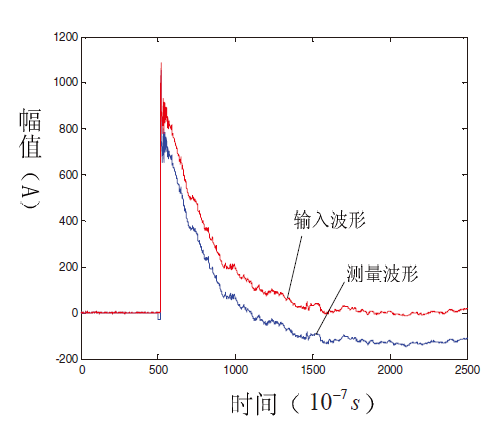
圖 4 校正前輸入波形和測(cè)量波形對(duì)比
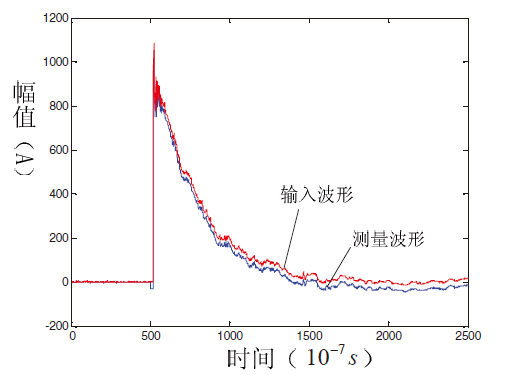
圖 5 校正后輸入波形和測(cè)量波形對(duì)比