由于積分器中的累積誤差的存在,該誤差消除一直是阻礙Rogowski 線圈電子式電流互感器大范圍工程應(yīng)用的一個重要問題,并且各種改進的積分算法也大多是圍繞抑制直流漂移而改進的。
目前消除累積型誤差主要有兩大類��,即抑制法和補償法��。常用的抑制法包括:
(1)在ADC 之后加裝數(shù)字式高通濾波器(High-pass Filter,HPF)�����;
(2)改變積分算法,抑制直流輸入。
現(xiàn)代的電力系統(tǒng)要求電流互感器能完整準確實時地反應(yīng)被測點的電流��,特別是要更精確的反應(yīng)諧波電流和暫態(tài)電流�����。所以以上方法在更嚴格的要求下會產(chǎn)生如下一些問題�。
(1)穩(wěn)態(tài)時會對積分器輸出的幅值和相位精度有一定的影響�����。蘇育均等提出的一種無限沖擊響應(yīng)(Infinite Impulse Response, IIR)數(shù)字濾波器�����,雖然能較好的濾除直流,但是其對輸出的相位精度影響較大。
(2)上述直流抑制方法是不加區(qū)分的濾除直流,當電力系統(tǒng)發(fā)生故障時�����,電網(wǎng)中電流存在非周期的爬升電流����,隨后這部分故障電流會發(fā)生衰減,這種變化形式的電流分量在經(jīng)過Rogowski 線圈之后變現(xiàn)為近似直流性質(zhì)的電壓信號,而這部分信號是不應(yīng)該被消除的��,否則會導致積分器輸出的電流值要小于實際被測點的電流值�,從而影響繼電保護的動作。
(3)從算法上抑制直流輸入也會對高次諧波的積分精度產(chǎn)生影響,例如朱超等[31]提出的將低頻增益平坦模擬積分器數(shù)字化的算法�,雖然將直流衰減到原來的1/4��,但是對高次諧波的測量精度影響較大。
所以,一個優(yōu)秀的誤差補償與消除的環(huán)節(jié)應(yīng)該是在完全保持原電流的微分信號不變的同時,消除ADC 及其前置電路中產(chǎn)生的所有包括直流在內(nèi)的誤差信號���。補償法,即在積分器輸入被積值時對其中的直流漂移進行補償,最簡單的補償量的確定可以通過查表獲得�,查表法的局限在于無法獲得每一個元器件的補償表��,僅能獲得整個批次或者該產(chǎn)品的補償表,并且由于元器件壽命的問題而產(chǎn)生的誤差更是無法在補償表中體現(xiàn),所以查表法的精度不高?����,F(xiàn)在一般使用的方法是實時計算均值獲得直流誤差來進行補償�,這種補償方法響應(yīng)速度慢,并且也容易對正常的輸入產(chǎn)生影響���。
另一類比較優(yōu)秀的補償方法是不確定數(shù)值關(guān)系的黑盒補償方法,主要有以下兩種:
(1)對地積分補償法,其采用一對參數(shù)相近的積分器��,當其中一個積分器對地積分時���,可以獲得b 值用于補償��。其缺點是由于一個積分器的輸入是零電位,其輸入功率明顯小于原信號積分器的輸入功率����,因此雖然兩組放大采樣電路參數(shù)一樣����,但是工況不同��,所產(chǎn)生的誤差并非完全一樣�,效果有限�。
(2)交叉反相采樣法,以固定頻率對原信號進行反相����,使反相后獲得的積分值與前段相同時間內(nèi)未反相的積分值獲得相同的偏移值����,進行處理后獲得偏移值并進行補償��。其缺點是頻繁地使用電力電子器件對原信號進行反相操作�,在反相時會對原信號產(chǎn)生畸變���,從而產(chǎn)生新的誤差����,并且實際操作上還存在一定的困難。
參考上述兩種模擬積分器誤差補償方法�,我們提出可應(yīng)用于數(shù)字積分器的一種簡單而實用的直流誤差消除方法——鏡像法����,具體方法如下�。首先對Rogowski 線圈出口電壓進行分壓處理以獲得兩個等幅而反相的電壓信號,分壓電路如圖1所示�����。
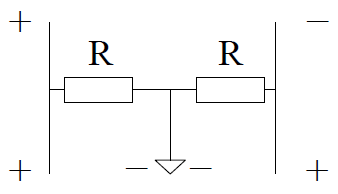
圖1分壓反相電路
再取兩套參數(shù)相同的ADC 及其前置放大電路并列運行�,輸入為該組等幅反相信號�,從而構(gòu)成鏡像輸入,最后將兩套裝置的出口數(shù)據(jù)進行差運算,具體流程如圖2所示(圖中放大采樣模塊的公共端連接已略去)��。
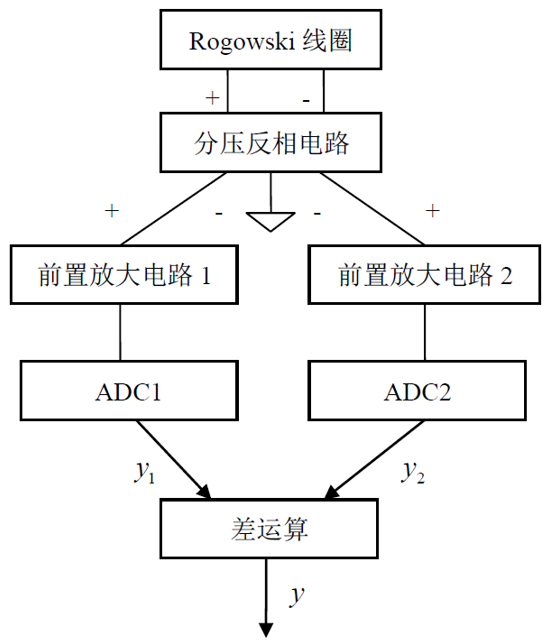
圖2鏡像消除誤差過程
ADC1 和ADC2 的出口值1 y , 2 y 為
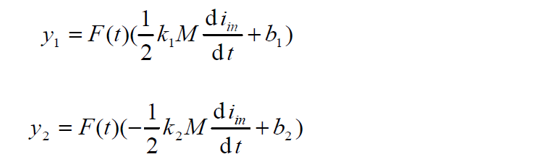
其中F(t)為采樣函數(shù)���, 1 2 k , k 分別為兩組放大采樣電路的綜合放大比, 1 2 b ,b 為ADC1 和ADC2 及其前置放大電路中產(chǎn)生的直流誤差�。
最終積分器的輸入值y 為
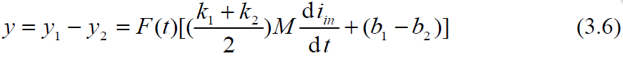
由于一對鏡像工作狀態(tài)的ADC 及其前置放大電路在生產(chǎn)條件����、運行環(huán)境���、輸入幅值等方面高度的一致性�����,所以認為有1 2 1 2 k ? k ,b ? b ���,從而

顯然�,該方案并不直接對1 y 、2 y 進行串聯(lián)性質(zhì)的濾波處理����,最大程度地保持了1 y ����、2 y 對一次電流值的真實反映����,在經(jīng)過復化梯形公式積分之后能真實準確地反映一次側(cè)電流在穩(wěn)態(tài)和暫態(tài)運行條件下、在基波和諧波上的各種特征。Rogowski 線圈不產(chǎn)生直流漂移�����,而數(shù)字電路部分無誤差���,從而積分器的被積函數(shù)完全是被測點電流的微分值的真實反映�。該方案有以下優(yōu)點:
(1)直流誤差消除效果較好;
(2)完整地保留被測電流的微分信號,被測電流中的低頻振蕩�、次諧波�、直流衰減電流時不會被錯誤的濾除�����;
(3)響應(yīng)速度極快���;
(4)對兩套ADC 采樣模塊的輸出進行比較��,如果某一套裝置發(fā)生故障���,則很容易發(fā)現(xiàn)數(shù)據(jù)異常而發(fā)出故障報警信號�,并閉鎖相應(yīng)的繼電保護裝置,提高了電網(wǎng)的穩(wěn)定性與可靠性;
(5)結(jié)構(gòu)簡單�,便于工業(yè)化生產(chǎn)。