數字積分器的誤差是制約Rogowski 線圈電子式電流互感器應用的重要因素之一。從來源上分析，Rogowski 線圈電子式電流互感器的四個模塊，即Rogowski 線圈、傳輸及放大模塊、ADC 采樣模塊、數值積分模塊，均會產生誤差。由于積分計算對一些誤差有累積作用，因此從誤差類型上分析，又可以分為累積型誤差和非累積型誤差，其中累積型誤差對積分器的性能產生巨大的影響，是誤差消除的重要部分。

對于由運放組成的放大電路和采樣電路，由于是線性電路，其輸入輸出關系可以近似用Texas Instruments（TI）公司使用的ADC 的輸入輸出關系圖（如圖1所示）表示。

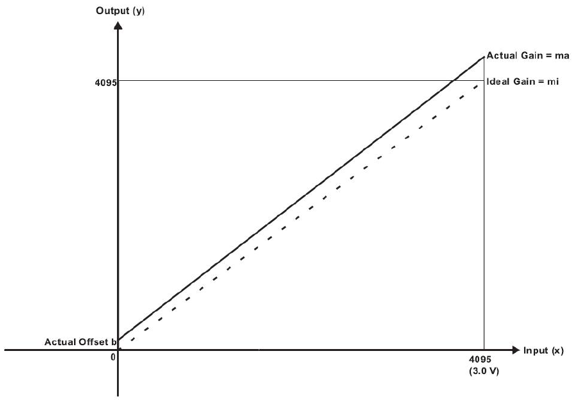
圖1 線性模擬電路輸入輸出關系圖

理想情況下輸入輸出關系為：

實際電路中輸入輸出關系為：

分別將式（3.1）（3.2）帶入式（1.1）中，并作差可得：

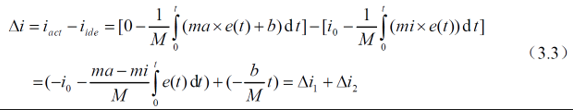
因此Rogowski 線圈電子式電流互感器要想在工程中大量應用，至少需要克服

以下三個方面的困難：

（1）ADC 采樣頻率、采樣范圍、采樣精度的限制。Rogowski 線圈電子式電流互感器需要測量范圍較大，在正常運行時的量程至少為1%~120%的額定電流，同時又要求保證測量故障電流的高精度，因此其ADC 裝置的采樣范圍較大。且無論采用哪種積分算法，其算法精度都與采樣頻率相關，越高的采樣頻率，與ADC 相連的積分環節的積分精度就越高，因此需要更高采樣頻率的ADC。同樣，ADC 的采樣器的精度誤差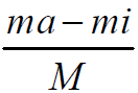直接關系到整個數字積分器的誤差，從而需要高精度高性能的ADC。

（2）積分初值0 i 的補償。任何一種積分算法在其積分初始時刻均無法獲得原電流值，若不加以補償，則積分環節出口的積分值比原電流小0 i （如圖2所示），因此數字積分器需要設計一套方法對積分初值進行準確有效地補償。

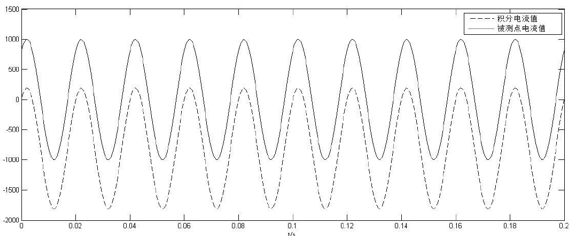
圖2未補償積分初值的積分器輸出與被測點電流比較圖

（3）積分環節輸入信號中的直流誤差b 的消除。由于ADC 及其前置放大電路中含有運放等受溫度、器件老化程度因素影響的模擬元器件，在ADC 的數字輸出中必然有一定的直流漂移，該直流漂移作為一個同極性的誤差輸入到積分環節會隨著時間而大量累積（如圖3所示），成為積分器較大的輸出誤差之一，若不加以消除，最終會導致積分環節的數據溢出。因此，需要對該直流誤差進行消除。

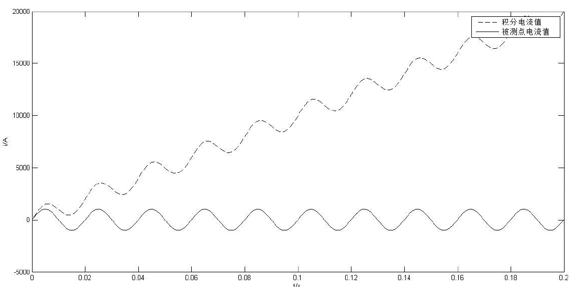
圖3 未濾除直流的積分電流值與被測點電流比較圖